Post

From Pedersen to Polynomial Commitment Scheme

Pedersen Commitment Scheme and Polynomial Commitment Scheme

Posted Updated
Preview Image
By wiimdy
10 min read
From Pedersen to Polynomial Commitment Scheme

From Pedersen to Polynomial Commitment Scheme

이번 글에서는 Pedersen Commitment Scheme와 Polynomial Commitment Scheme에 대해 설명하겠습니다.

들어가기전에 간단하게 Commitment에 설명하자면, value와 salt를 통해 commit 한 후 reveal을 통해 (value, salt) 쌍을 공개합니다.

이를 통해 committer는 value를 원하는 때 공개하며 value를 알고 있었음을 증명할 수 있습니다.

commitment로 value를 추측하지 못하는 Hiding 속성을 만족해야 하고 committer는 동일한 commit이 나오는 (value, salt) 쌍을 찾을 수 없어야 하는 Binding 속성을 만족 해야합니다.

Pedersen Commitment Scheme


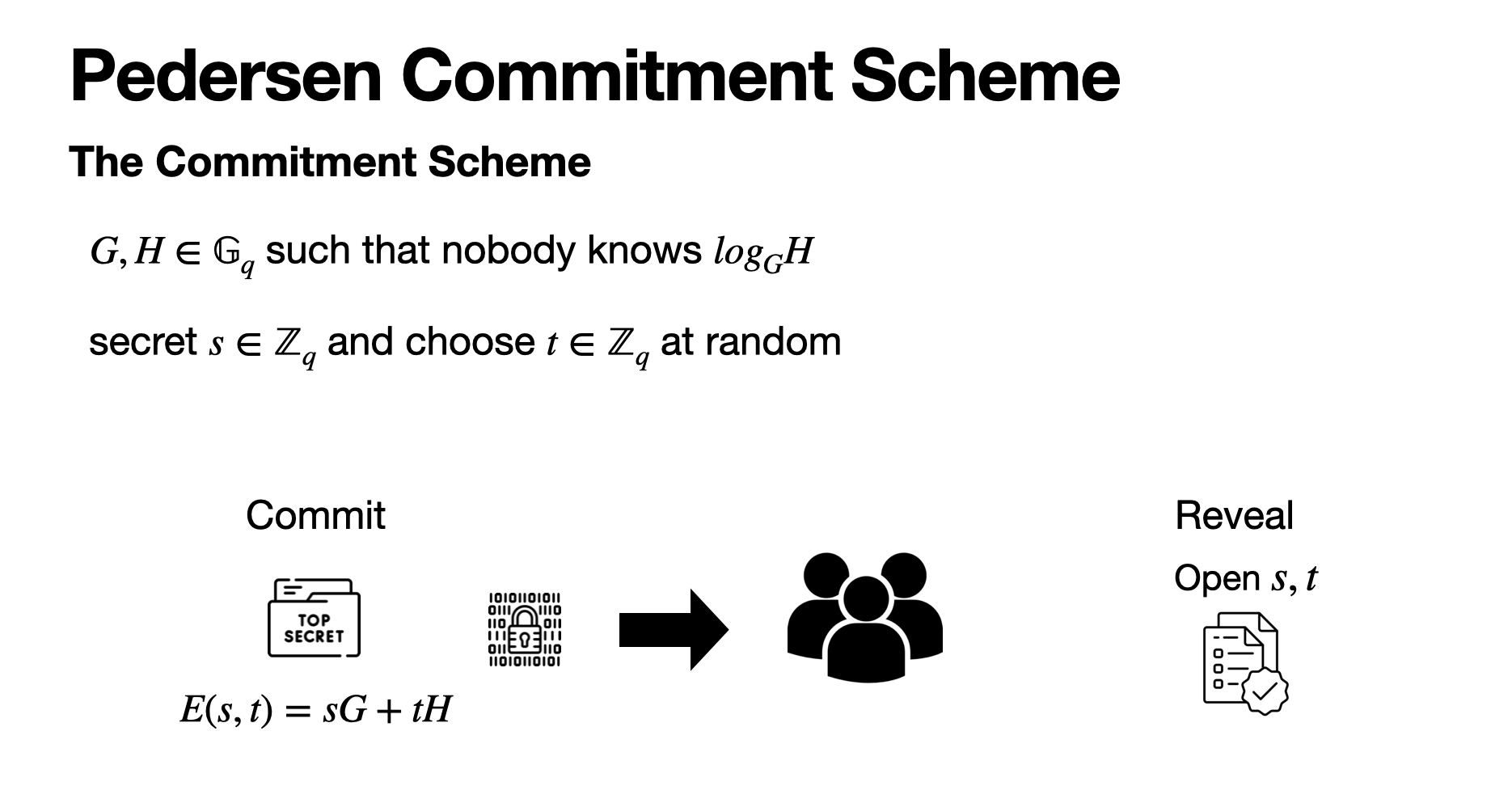
Pedersen Commitment는 타원곡선을 이용해서 commitment를 진행합니다.
타원곡선상의 랜덤한 두 점인 \[ G, H \]를 골라 두 점의 이산 로그 관계를 알 수 없어야 합니다.
(\[ H = xG\] 를 만족하는 x를 구할 수 없어야 합니다.)

salt 값으로 사용하는 t를 랜덤으로 뽑고 비밀 값인 s와 연산을 진행합니다.
Commitment: \[ E(s,t) = sG + tH\]

이 값을 verifier에게 전달한 후 reveal을 진행하여 (s, t)를 공개합니다.

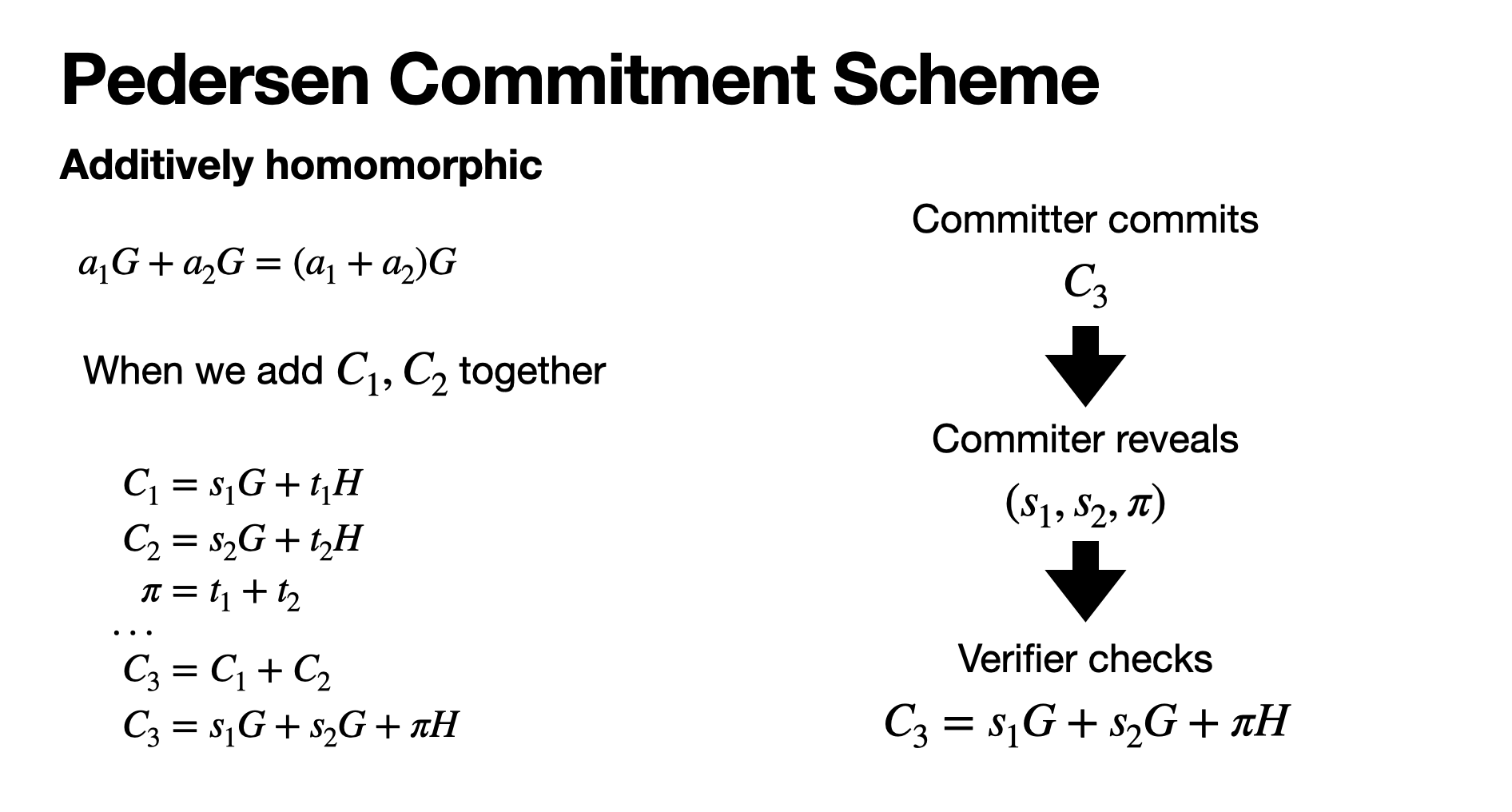
Additively homomorphic

일반적으로 commitment를 진행할 때 hash 함수를 많이 사용하는데 hash 함수와 달리 타원곡선 상의 연산을 이용하기 때문에 덧셈 연산에 동형 성질을 가집니다.
따라서 commitment \[ C_1, C_2\] 에 대해 한번에 검증하기 위해 두 commitments를 더해서 검증을 진행합니다.
이때 blinding factor인 \[ t_1, t_2 \] 는 더해 (\[ s_1, s_2, \pi \]) 를 reveal 합니다.

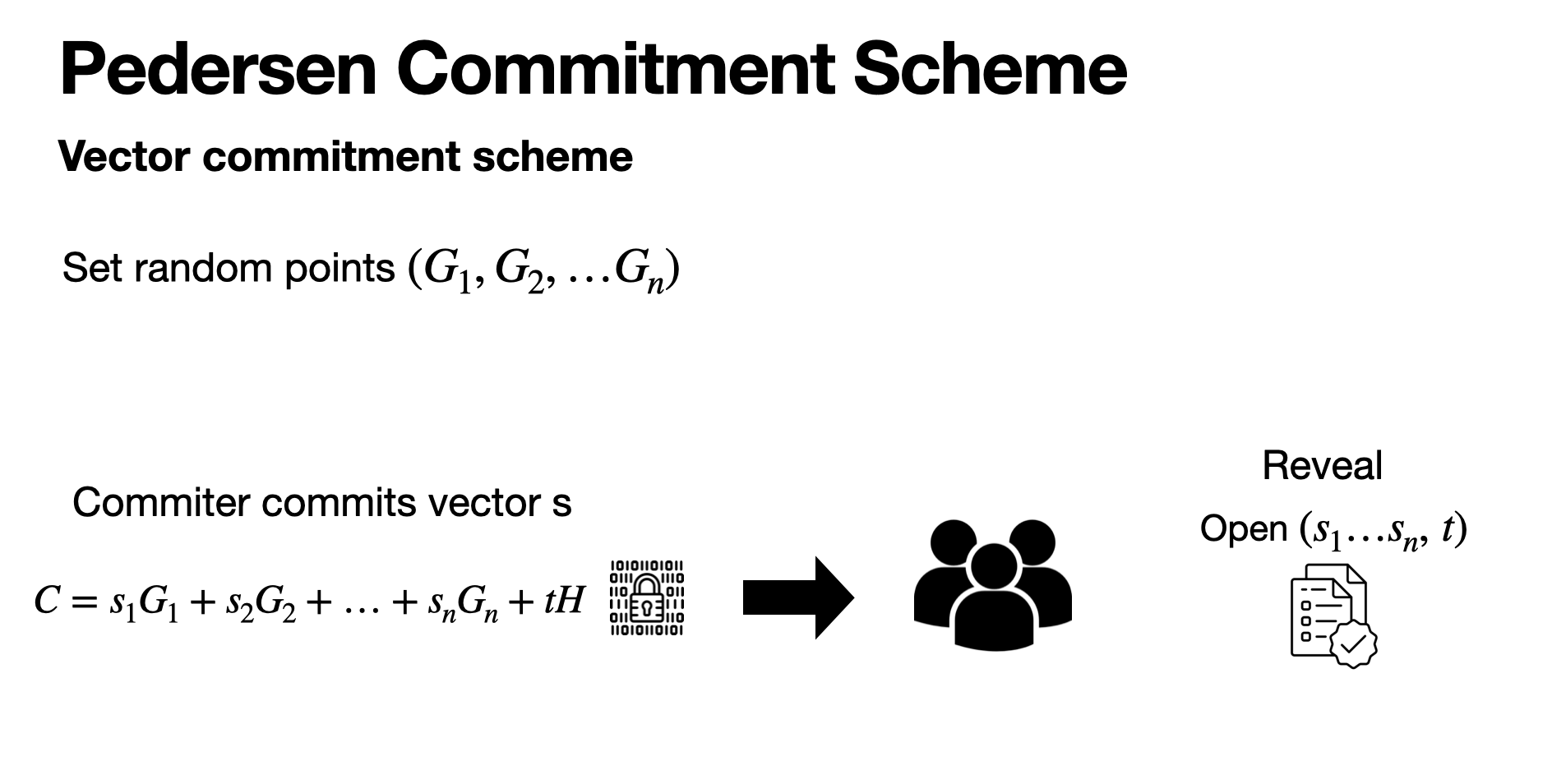
Vector commitments

타원곡선의 점을 여러개 잡으면 벡터 s를 스칼라 곱으로 계산할 수 있다. 즉 벡터 s를 비밀 값으로 commit 할 수 있습니다.
나머지 과정은 동일하게 진행합니다.

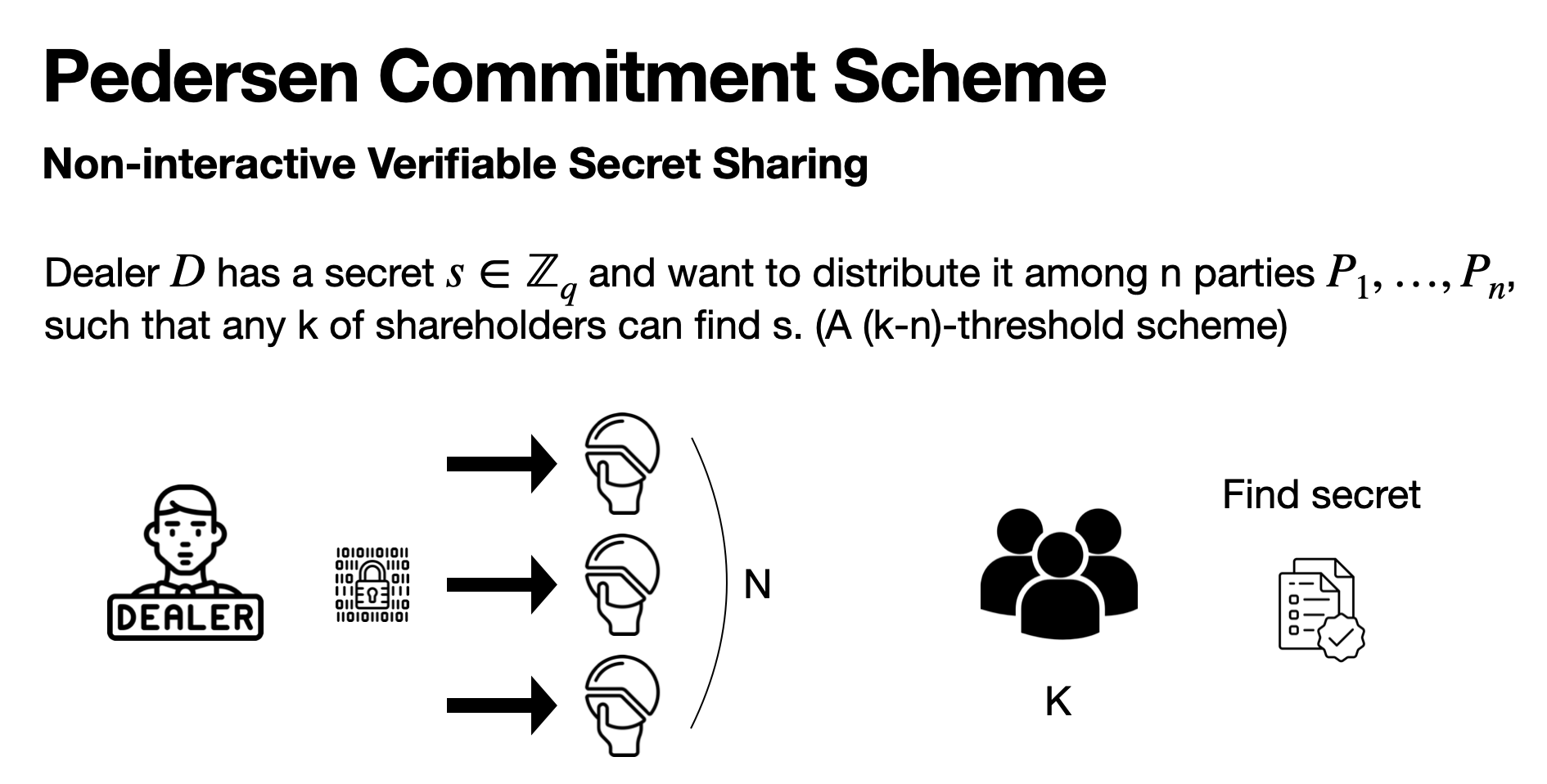
Non-interactive Verifiable Secret Sharing

Pedersen Commitment는 사실 non-interactive하게 비밀을 공유하고 그걸 검증하는 scheme의 기반이 되는 기술입니다. 비밀 s를 나누어 n명의 사람에게 나누어주고, 이 몫을 가지고 있는 사람들은 이 몫이 옳은지 검증할 수 있어야 하고, 또 k 이상의 사람이 모였을 때 비밀 s 값을 알 수 있습니다.

딜러는 다항식 \[ \phi(0) = s \] 를 만족하는 (k - 1)차 다항식을 만듭니다. 그리고 사람들에게 \[ \phi(i) \] 의 값을 비밀의 몫으로 나누어줍니다.
이 몫으로는 비밀 값 s에 대한 정보를 얻을 수 없습니다.
몫을 가진 사람이 k명 이상 모였다면, 라그랑주 보간법에 의해 k개의 점으로 (k - 1)차 다항식을 만들 수 있습니다.

몫을 받은 사람은 자신이 받은 \[\phi(i) \] 값이 진짜 다항식의 evaluation인지 확인해야 합니다.
이러한 과정을 Polynomial Commitment 통해 진행할 수 있습니다.

Polynomial Commitment Scheme

Polynomial Commitment는 앞서 말한거처럼 committer는 다항식을 알고 있다는 것을 보여줘야 합니다.
그리고 랜덤 값인 \[u\]에 대해 evaulation인 \[\phi(u)\]의 값을 증명할 수 있어야 합니다.
이 과정에서 다항식에 대한 정보가 노출되면 안됩니다.

Constant size commitments

첫번째 방법은 다항식의 계수를 string으로 만들어 commitment를 진행하는겁니다.
이 방식은 Constant size commitment 이기 때문에 communication 과정에서 overhead가 적습니다.
하지만 \[\phi(u)\]를 증명하는 과정에서 string 전체를 보여줘 다항식의 정보가 노출되기 때문에 암호적으로, 특히 secret sharing scheme에서는 적절하지 않습니다.

Coefficient commitments

전체 다항식을 한번에 commitment 하지 않고 계수마다 나누어서 진행하는 방법입니다.
commitment 값을 선형결합을 통해 \[\phi(u)\] 를 증명자가 검증할 수 있습니다.

Pedersen & Polynomial Commitment Scheme


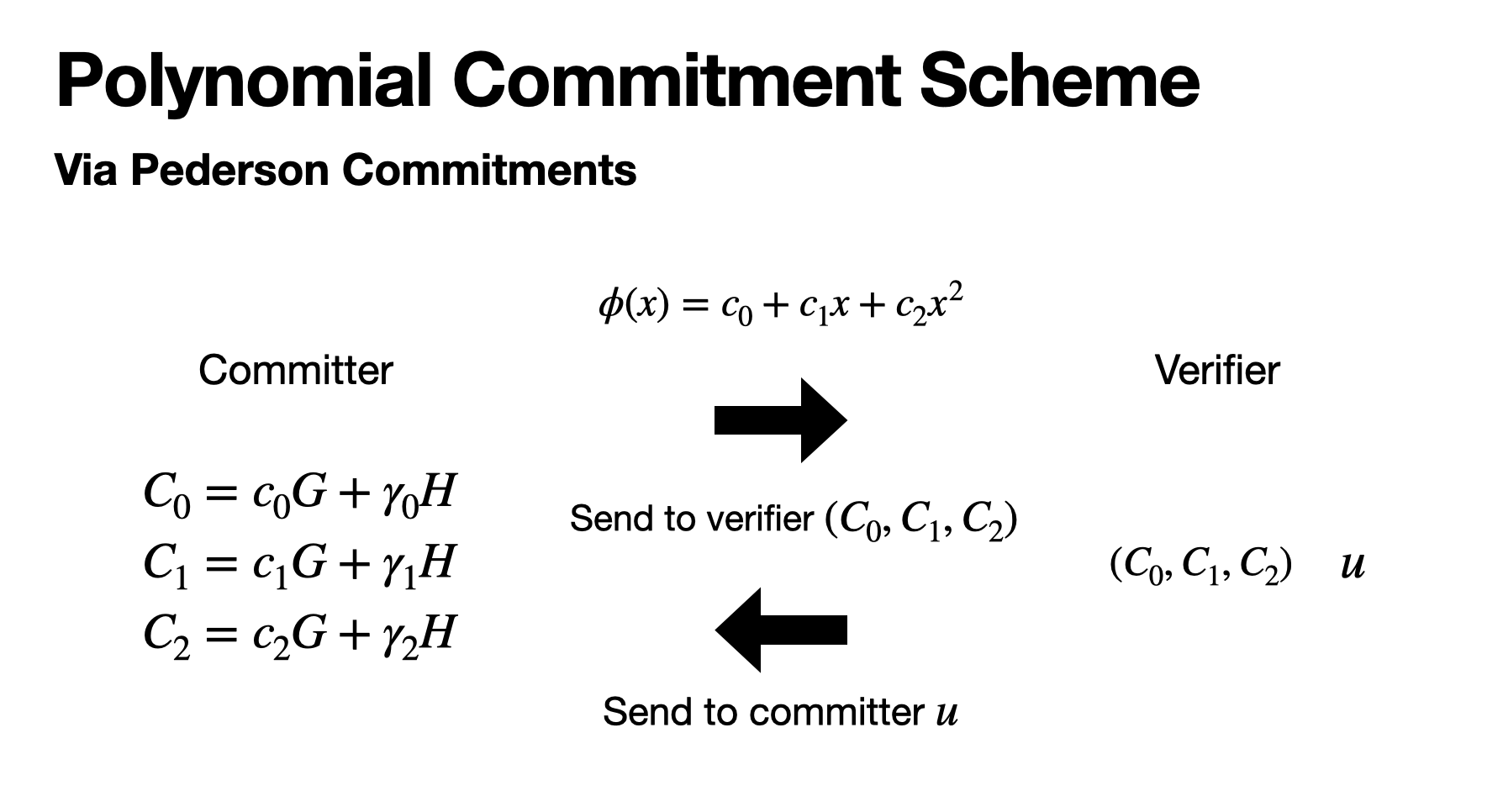
계수들을 commitment 하는 것은 Pedersen commitment로부터 영감받았습니다.

위의 계수 commitment 하는 과정에서 salt를 추가하면 어떻게 바뀌는지 살펴보겠습니다.

계수들을 벡터로 보아 Pedersen commitment를 진행합니다.
여기서는 interactive로 evalutate하는 값인 u를 verifier에게 받습니다.


committer는 \[\phi(u) \] 값과 blinding factor와 u가 결합된 \[\pi\] 를 계산해서 verifier에게 전달합니다.
\[\pi\]를 저렇게 계산한 이유는 검증과정에서 필요하기 때문입니다.

Verification

좌변에서는 \[C_0, C_1, C_2\]에는 계수와 은닉 요소가 있기 때문에 u와 조합을 하면 다항식에 대한 평가값의 commitment가 나옵니다.
우변에서는 다항식에 대해 평가값과 \[\pi\]를 쌍으로 한 commitment 값이 나옵니다.

따라서 committer가 올바르게 \[\phi(u)와 \pi\]를 계산하여 보낸다면 증명이 통과됩니다.

Why the committer cannot cheat

만약 committer가 올바르지 않은 다항식의 평가값을 전달한다면 해당 검증식을 통과하기 위해 \[\pi \prime\] 을 만들어야 합니다.
하지만 식을 전개해보면 \[G, H\]의 관계식이 나오기 때문에 두 점의 이산로그 관계를 모른다면 \[\pi \prime\] 만들 수가 없습니다.
따라서 \[G, H\]의 이산로그 관계는 아무도 몰라야 안전한 commitment scheme이 됩니다.

Summary

이 commitment scheme은 blinding factor를 연산에 넣어 hiding을 만족하고, G와 H의 이산로그 관계를 committer가 모른다면 거짓을 전달하지 못해 두가지 성질을 만족합니다.

하지만 commitment의 개수가 n에 비례하기 때문에 communication overhead가 O(n)이 됩니다.
따라서 constant commitment를 달성할 수 있는 commitment scheme을 사용하면 더 효율적일 수 있습니다.

KZG Polynomial Commitment

KZG Polynomial Commitment는 communication 과정에서 생기는 cost와 complexity를 줄이기 위해 만들어졌습니다.
Setup 과정을 통해 한번 쓰고 버리는 값으로 PK를 만들고 PK를 이용해서 commitment를 진행합니다.

다항식 전체를 open하냐, 아님 다항식을 알고 있음을 증명하는 임의의 값에서 평가를 open 하냐 두 가지로 나누어집니다.

첫번째 방식으로 다항식을 공개하여 verifier가 commitment를 계산하여 일치하는지 확인합니다.

다른 방식으로는 committer가 랜덤한 값을 다항식에 evaluate한 값을 만듭니다. \[\phi(i) = y\].
그럼 이 값이 commit 한 다항식에 넣은 값인지 증명하는 proof 인 \[\omega_i\]를 만듭니다.

이 값을 verifier에게 전달하여 \[\phi(i)\] 가 commit 한 다항식에 넣은 값이 맞는지 proof 를 통해 검증을 진행합니다.

Reference

Crypto
ZK, Commit
This post is licensed under CC BY 4.0 by the author.