DLP-based Public-Key Cryptography

DLP-based Public-Key Cryptography

이 아티클에서는 이산 로그 문제를 기반으로 하는 공개키 암호에 대해 다루도록 하겠습니다.

Discrete Log Problem (DLP)

많은 암호 시스템들은 이산 로그 문제 (DLP) 를 기반으로 보안성을 보장하고 있습니다.

DLP 는 다음과 같이 정의할 수 있습니다.

$ \begin {aligned} &\text {Given group G is cyclic, with G } = \langle g \rangle \; \text { and } a \in G \\ \\
& g^x \equiv a \ (mod \ p) \qquad \text {It is easy to find “a” given (g, x, p)} \\ \\
& ind_ga \equiv x \ (mod\;p) \qquad \text{But it is hard to find “x” given (g, a, p)} \end {aligned} $

g가 premitive roots 이고 group 안에 있는 a에 대해 \[ g^x \equiv a \ (mod \ p) \] 를 만족하는 x를 찾기 어렵다는 문제입니다.
x를 구하기 위해 로그의 형태를 씌워서 \[ ind_ga \equiv x \ (mod\;p) \] 이산 로그 문제라고 불립니다.

왜 이 문제를 풀기 어렵나고 하면 premitive roots의 성질로 G안에 있는 원소들은 합동이 아닙니다.
따라서 a는 G안에 하나만 존재합니다.
또한 \[ if\; a < b, \quad g^a \nless g^b \; (mod \; p) \] 이기 때문에 G안에 원소의 규칙이 없는 상태입니다.

p가 Large prime이기 때문에 약 2^2048이기 때문에 현재 가장 빠른 알고리즘인 Pohlig-Hellman algorithm를 통해 찾아도 시간 복잡도가 \[ O(\sqrt n) \] 이기 때문에 10^300 정도의 연산이 진행됩니다.
따라서 이 문제가 어려운 이유는 p가 large prime일 경우 규칙 없이 연산을 많은 횟수로 진행하기 때문이다.

---

Diffie-Hellman key exchange

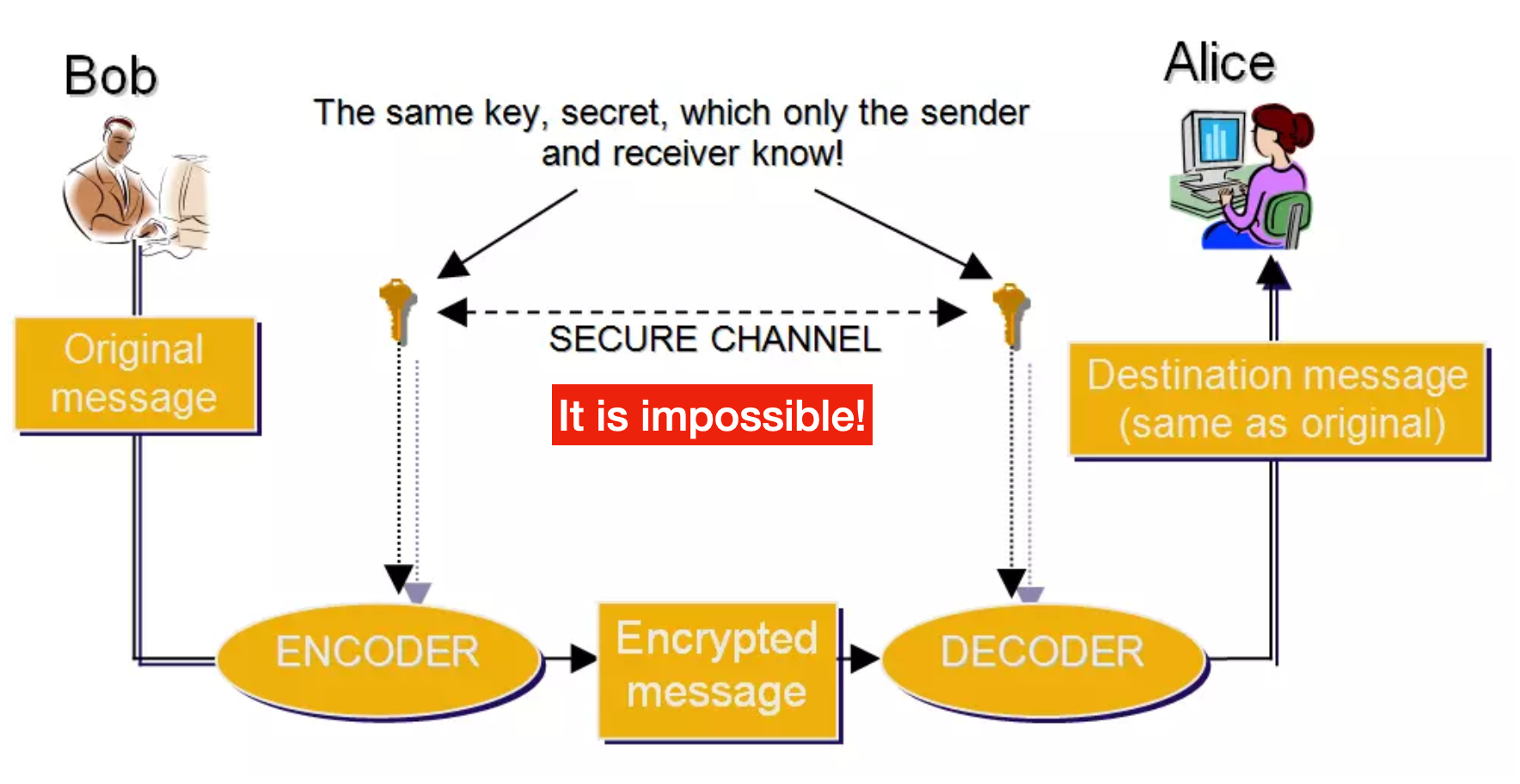
과거의 대칭키의 키 교환을 진행할 때 안전한 채널에서 진행해야 합니다.
하지만 안전한 채널이라는 것이 불가능하기 때문에 키 교환에 위험이 따랐습니다.

Diffie-Hellman 키 교환 방법은 공개키를 이용하여 동일한 비밀키를 만듭니다.

이를 통해 대칭키 암호화 방식의 문제점인 비밀키 교환을 하지 않고 공개키를 교환하여 비밀키를 만듭니다.

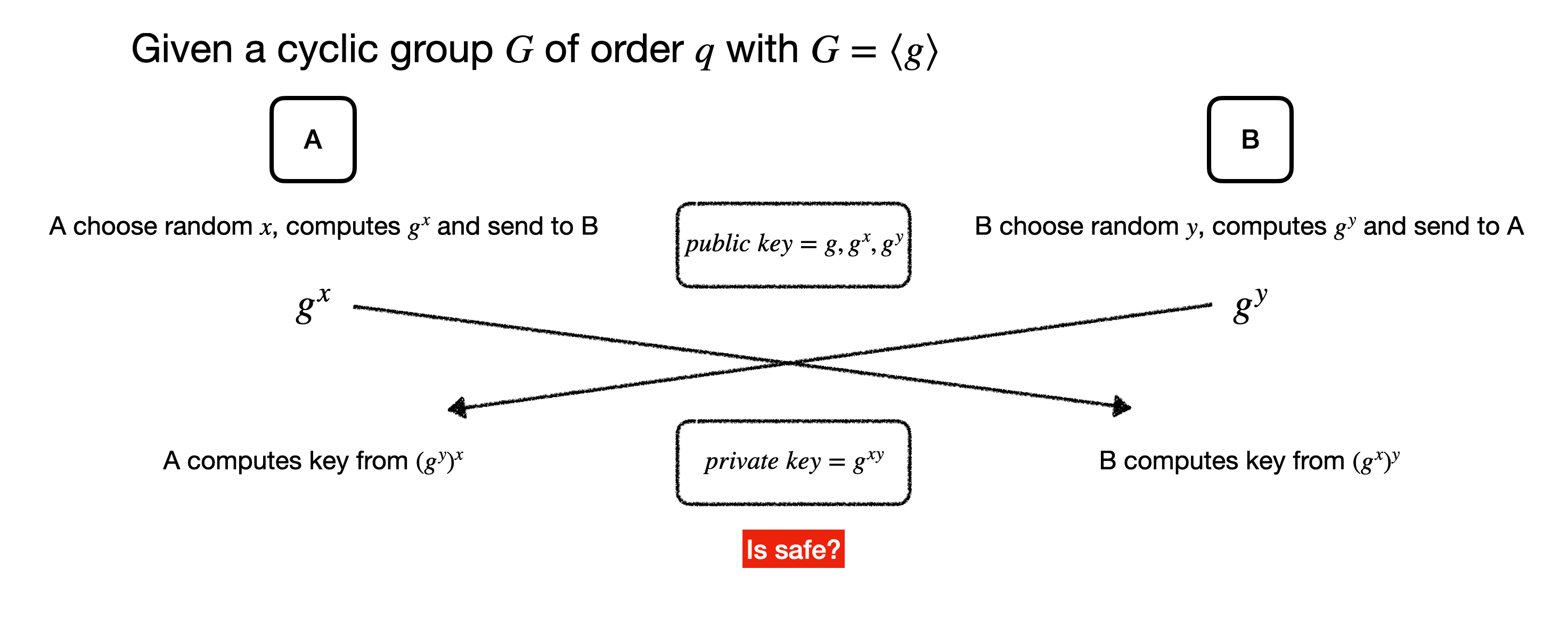
1. A chooses a random integer x with 0 < x < M (Large Num), computes \[g^x\], and sends the result to B, keeping x secret.
2. B chooses a random integer y with 0 < y < M (Large Num), computes \[g^y\], and sends the result to A, keeping y secret.
3. Both A and B construct the key from \[g^{xy}\], which A computes from \[(g^y)^x\], and B computes from \[(g^x)^y\].

이 암호 시스템이 안전한가는, 공개키를 통해 개인키가 계산되면 안됩니다.

$ \begin {aligned} g^{xy} \;\text {from knowledge of } g, g^x \text{ and } g^y \text { should be intractable.} \end {aligned} $

위의 문제가 Diffie-Hellman Problem 으로, DLP를 해결 할 수 있다면 Diffie-Hellman Problem을 풀 수 있습니다.

---

ElGamal Encryption

이 암호 시스템은 Diffie-Hellman의 공개키 개념을 제시한 이후 등장한 공개키 암호 시스템 중 하나입니다.
유한체상에서 로그를 계산하는 것의 어려움에 기반을 둔 시스템입니다.

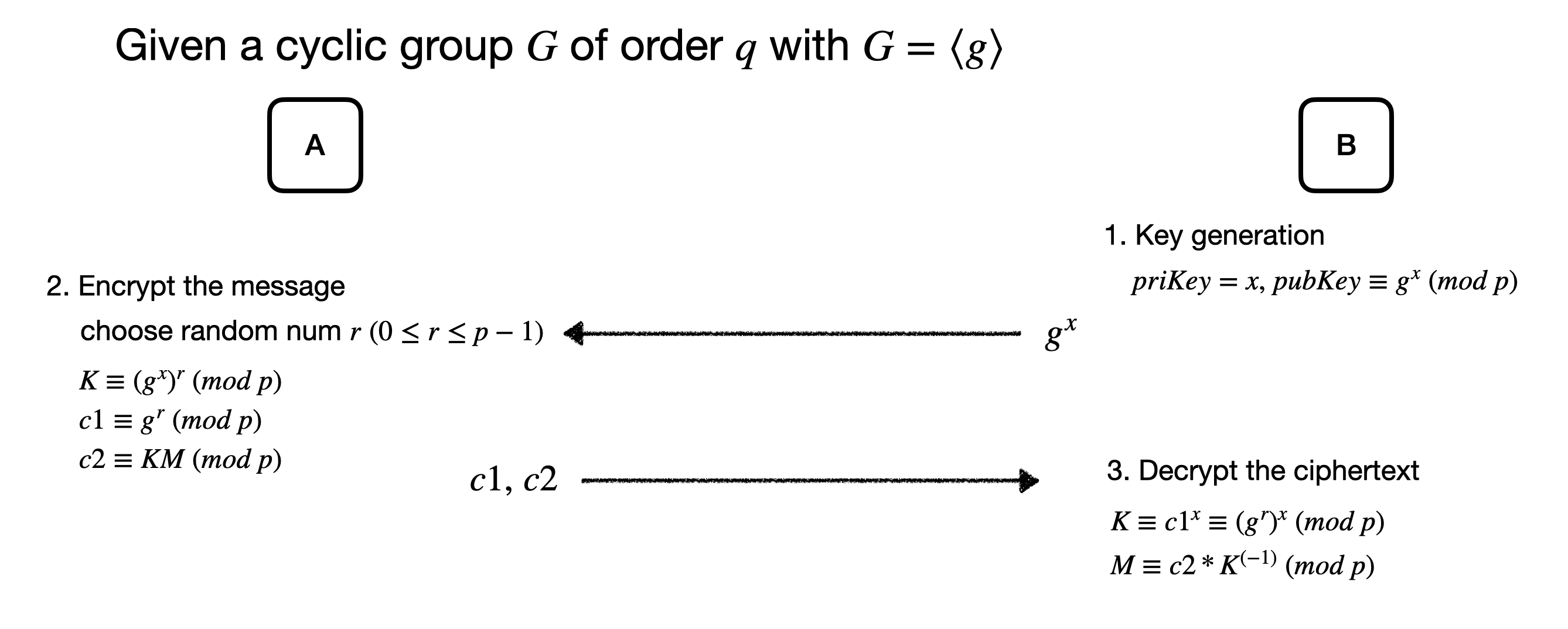
1. B의 키 생성: \[ priKey = x,\; pubKey \equiv g^{x} \; (mod \;p)\]
2. A의 메세지 암호화 (B의 공개키를 이용해서): choose random num r \[ K \equiv (g^x)^r\; (mod \; p) \qquad c1 \equiv g^r\; (mod\; p) \qquad c2 \equiv K M\; (mod\; p) \]
3. B의 암호문 복호화: \[c1^x \equiv (g^r)^x \equiv K \;(mod\; p), \quad c2* K^{(-1)} \; (mod\; p)\equiv M \]

A가 만약 랜덤값 r을 중복으로 사용하여 메세지를 암호화 하였을 때 생기는 경우이다.

만약 메세지 중 하나가 leak이 된다면 다른 메세지를 복호화 할 수 있기 때문에 랜덤 키 재사용을 권장하진 않는다.

---

Reference

• The Discrete Logarithm Problem, KEVIN S. McCURLEY, Proceedings of the Symposia in Applied Mathematics, vol. 42, 1990, pp. 49-74.
• New Directions in Cryptography, Whitfield Diffie and Martin E. Hellman, IEEE Transactions on Information Theory, Vol. IT-22, No. 6, 1976, pp. 644-655.
• A PUBLIC KEY CRYPTOSYSTEM AND A SIGNATURE SCHEME BASED ON DISCRETE LOGARITHMS, Taher ElGamal, IEEE Transactions on Information Theory, Vol. 31, No. 4, 1985, pp. 469-472.