ZK-SNARK based on the Decipher ZK Session
ZK-SNARK
ZK-SNARK based on the Decipher ZK Session
이 아티클에서는 Decipher ZK Session를 참조하여 ZK와 SNARK에 대한 기본적인 개념, ZK-SNARK의 과정에 대해 설명하겠습니다.
Zero-Knowledge
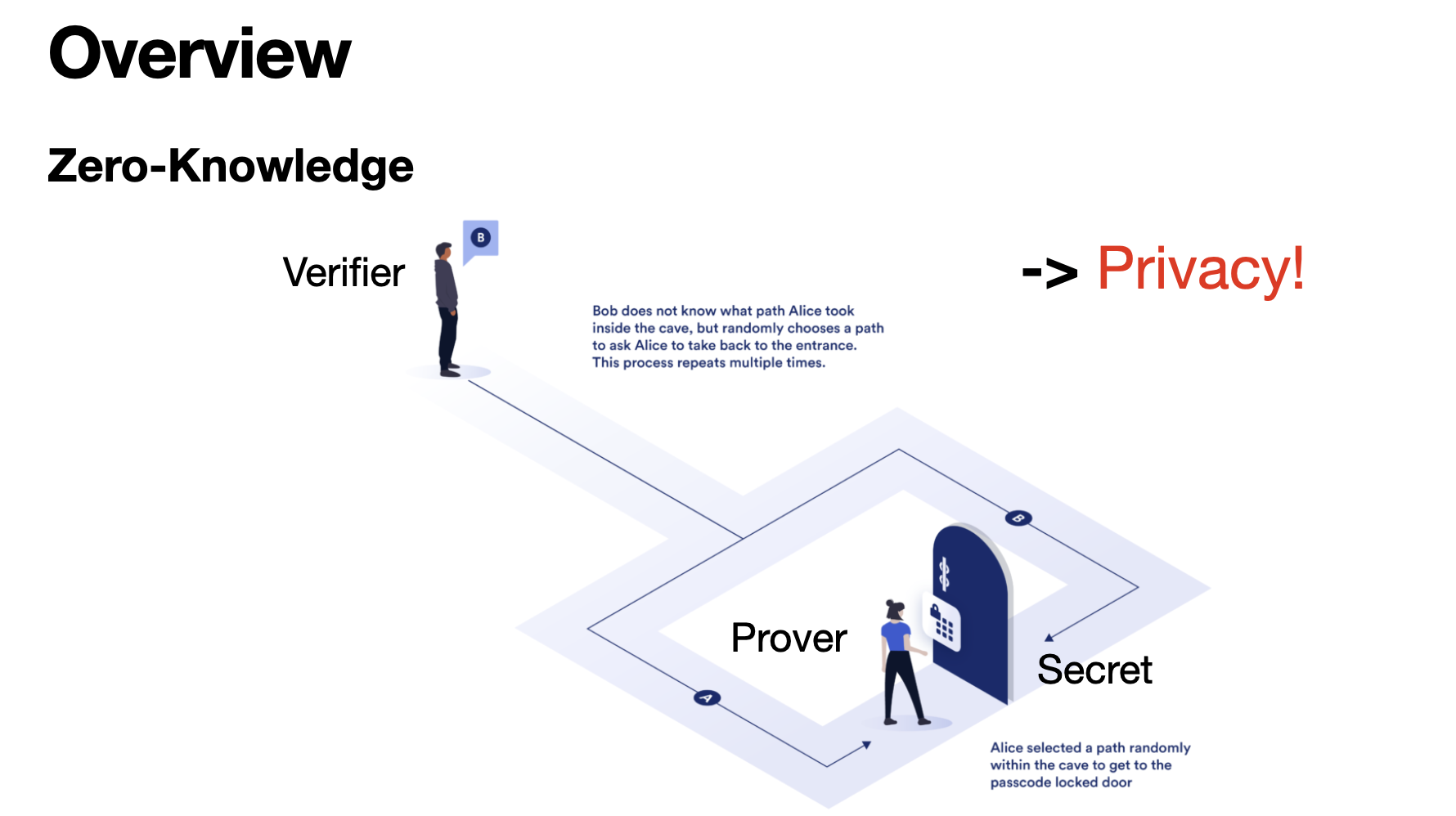
Zero-Knowledge란 Prover가 secret에 대해 정보를 주지않고, Verifier에게 secret을 알고 있음을 보여주는 개념입니다.
알리바바 동굴을 예시로 들면, 동굴 안의 Prover는 어느 방향으로 가도 secret을 알아 동굴 문을 열고 나갈 수 있습니다.
이 과정에서 secret은 노출되지 않고 알고 있음을 증명 할 수 있습니다. 뻔하지만 zk는 다음 3가지 성질이 있습니다.
- 완전성(completeness): 어떤 문장이 참이면, 정직한 prover는 정직한 verifier에게 이 사실을 납득 시킬 수 있어야 한다.
- 건실성(soundness): 어떤 문장이 거짓이면, 어떠한 부정직한 prover라도 정직한 verifier에게 이 문장이 사실이라고 납득 시킬 수 없어야 한다.
- 영지식성(zero-knowledgeness): 어떤 문장이 참이면, verifier는 문장의 참/거짓 이외에는 아무것도 알 수 없어야 한다.
SNARK: Succint Non-Interactive Argument of Knowledge
SNARK는 지식에 대한 증명을 비대화형으로 간결하게 하는 방법입니다.
예시로 “신뢰할 수 있는 PC”에서 “복잡한 연산”을 할 수 없어서 “믿을 수 없는 슈퍼컴퓨터”에서 진행한 연산의 증명을 “간결하게” 만들어 PC에서 검증하는 과정입니다.
이것이 곧 “off-chain에서” 실행한 transactions의 증명을 간결하게 만들어 Layer-1 에서 검증하는거와 일치합니다.
“ZK” + “SNARK” = “ZK-SNARK”
ZK-SNARK는 SNARK의 효율적이고 간결한 특성을 가지면서, 동시에 ZK라는 프라이버시 성질을 만족시키는 구체적인 영지식 증명 기술입니다.
예시로 private한 tx를 만든 “Tornado Cash”와 멤버십 인증을 하는 “Semaphore” 프로토콜이 있고, Scaling에 초점을 둔 “ZK-Rollup” 방식이 있습니다.
ZK-SNARK Process
ZK-SNARK는 어떤 함수나, 프로그램에 대해 input => output을 안다는 명제를 증명하기 위해 사용됩니다.
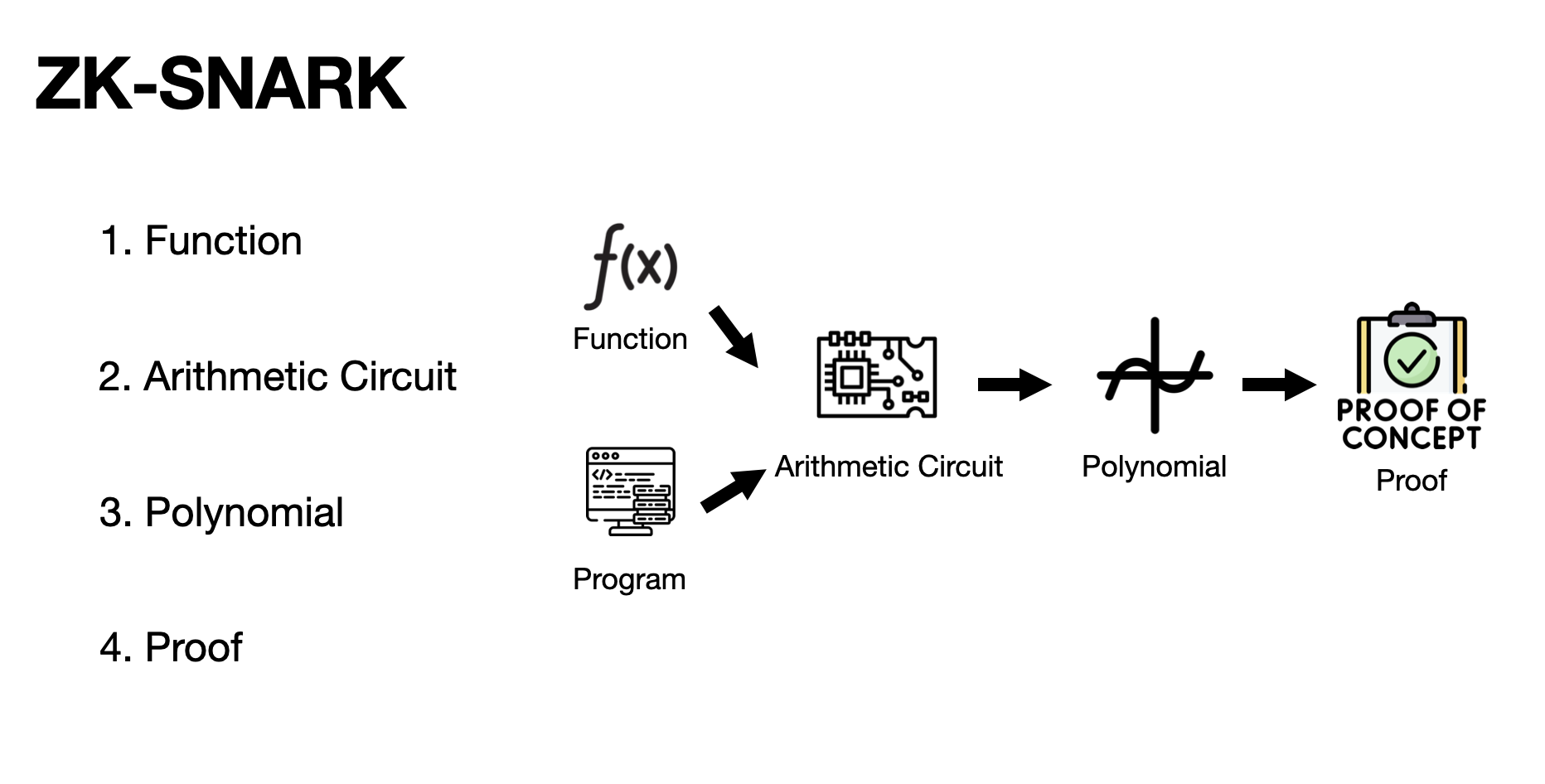
그래서 ZK-SNARK는 다음의 과정을 통해 증명을 진행합니다.
- 함수나 프로그램을 “Flattening” 과정을 통해 특정한 “Arithmetic circuit” 으로 변환합니다.
- Arithmetic circuit을 모아 암호학적 성질을 사용하기 편한 “Polynomial”로 변환합니다.
- Polynomial에 “Commitment”를 통해 Verifier에게 검증을 받습니다.
ZK-SNARK는 각 구성 단계에 필요한 암호학적 기법(Scheme)들을 모듈처럼 조합하여 다양하게 구현할 수 있습니다.
그 중 “R1CS”, “QAP”, “KZG Commitment”를 사용하여 증명을 하는 방식에 대해 설명드리겠습니다.
Function to Arithmetic Circuit
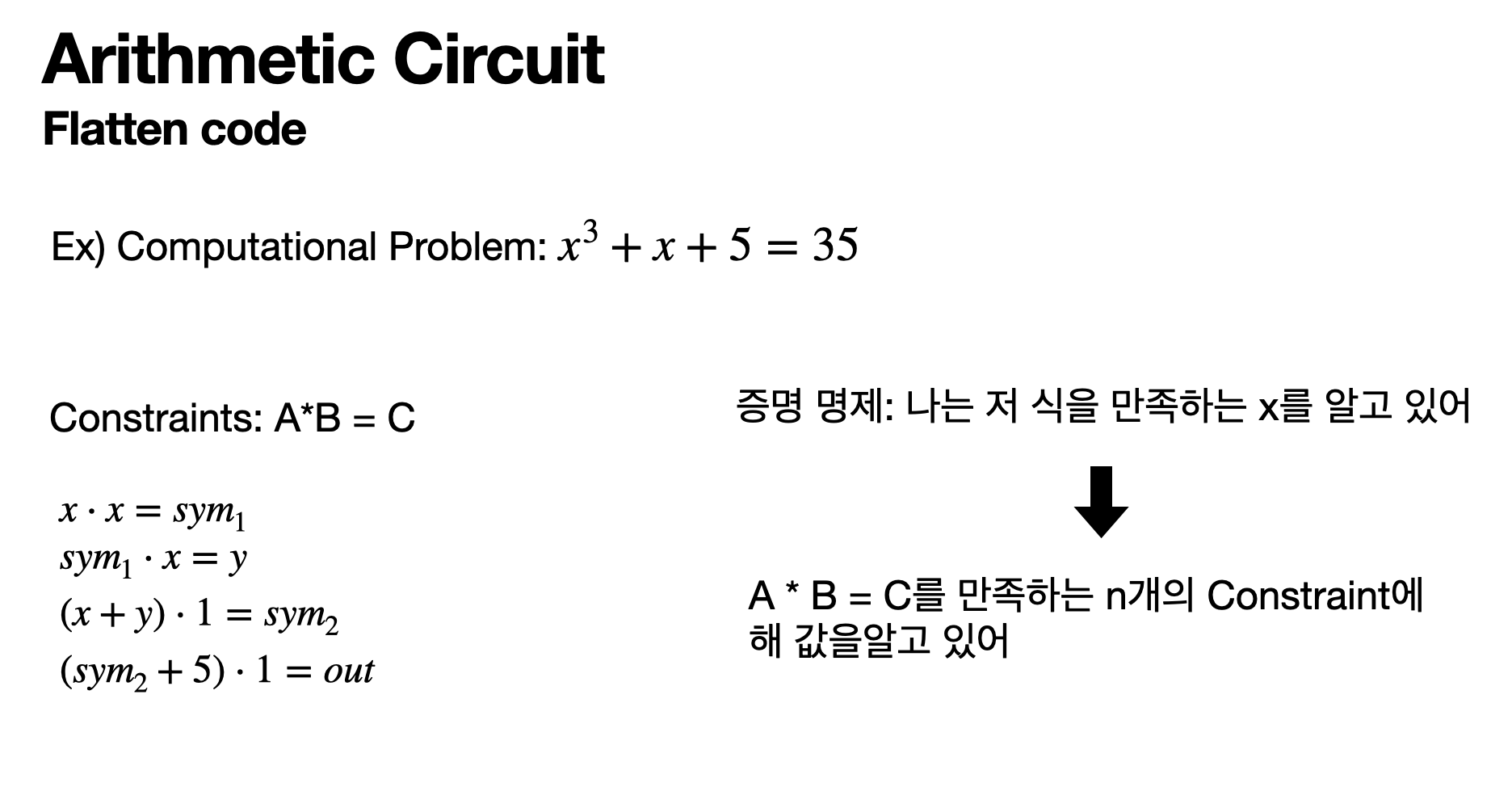
Function: “\[ x^3 + x + 5 = 35 \] 라는 식을 만족하는 \[ x \]를 안다” 라는 명제를 증명하고 싶습니다.
이 식의 답을 공개하지 않고 간결하게 비대화형으로 증명 해야합니다.
첫 번째 과정은 해당 함수를 “Constraints”로 바꾸는 겁니다.
R1CS를 사용할 것이기 때문에 \[ A\;*B = C \] 라는 형태의 constraint로 바꿉니다.
그럼 함수가 4개의 constraints로 바뀌게 됩니다.
\[\begin {aligned}
&x \cdot x = sym_1 \\ \
&sym_1 \cdot x = y \\ \
&(x + y) \cdot 1 = sym_2 \\ \
&(sym_2 + 5) \cdot 1 = out
\end {aligned}\]
Arithmetic Circuit to R1CS
- 우리는 만들어진 Circuit을 이용하여 \[ s \cdot a \times s \cdot b - s\cdot c = 0 \]을 만족하는 세 벡터 (a, b, c)를 만들겁니다.
\[ s = [~one, x, ~out, sym_1, \;y, \;sym_2\;] \] 는 solution vector로 Prover가 답을 알고 있다라는 것을 증명합니다. 세 벡터는 s 에서 필요한 값을 선택하는 역할을 합니다.
circuit 1: \[ x * x = sym_1 \] 에 대해 벡터 a, b는 x를 고르고 벡터 c는 \[ sym_1 \] 을 고릅니다. \[ a = [0, \;1, \;0, \;0, \;0, \;0] \] \[ c = [0, \;0, \;0, \;1, \;0, \;0] \]
다른 circuit들도 동일한 방법으로 진행하면 \[ s \cdot a \times s \cdot b - s\cdot c = 0 \]를 만족하는 세 벡터 (a, b, c)를 만듭니다.
각 circuit에서 만든 a, b, c를 순서대로 쌓아 행렬 A, B, C를 만듭니다.
그럼 R1CS 형태인 \[ s \cdot A \times s \cdot B - s\cdot C = 0 \]를 만족하게 됩니다.
R1CS to QAP
행렬 형태로 표현된 여러개의 constraints들을 하나의 다항식으로 압축하는 단계입니다.
R1CS의 행렬의 row는 constraint 하나를 의미합니다. 이 constraint 하나에 x = 1 과 같이 할당합니다.
다음으로 행렬의 각 column을 하나의 다항식으로 바꿉니다.
이는 다항식 보간법을 이용하여 이루워지고 우리는 라그랑주 보간법(Lagrange Interpolation)를 이용합니다.
예시로 \[ A_1(x) \] 는 (1, 0), (2, 0), (3, 0), (4, 5)를 지난다는 것을 알 수 있습니다. 그래서 이 네점을 지나는 하나의 삼차 방정식을 구합니다.
라그랑주 보간법은 위의 그림과 같이 진행합니다.
\[ A_1(x), \;A_2(x), \;A_3(x), … , \;C_6(x) \] 총 18개의 식을 만들어
\[ \Sigma_{i=1}^6(A_i(x)\cdot s_i) \times \Sigma_{i=1}^6(B_i(x)\cdot s_i) = \Sigma_{i=1}^6(C_i(x)\cdot s_i) \] 을 구합니다.
위 식은 \[ x = 1, 2, 3, 4\] 일 때 0을 지나므로 \[ (x-1)(x-2)(x-3)(x-4)Z(x) \] 로 표현할 수 있습니다.
여기까지 진행하면 처음 함수의 x 값을 알고 있다는 명제에서, R1CS를 만족하는 벡터 s를 안다,
\[ (A(x) * B(x) - C(x)) / (x-1)(x-2)(x-3)(x-4) \] 가 \[ Z(x) \]로 나누어 떨어진다 라는 명제로 바뀌게 됩니다.
따라서 Prover는 \[ Z(x) \] 에 대해 알고 있다를 증명하면 됩니다.
KZG Commitment
우리는 다항식을 Commit하는 방식 중 하나인 KZG Commitment를 사용할 것입니다..
\[ \phi(x) \in \mathbb Z_p[x], \quad \phi(x) = (\phi(x) - \phi(i))Q(x) \]
“계수가 유한체 \[ \mathbb Z_p \]에 속하는 방정식 \[ \phi(x) \]의 해 중 하나가 \[ i \] 일 때 \[ \phi(x) \] 는 \[ \phi(x) - \phi(i) \]로 나누어 떨어진다” 라는 속성을 기반으로 하고 있습니.
1. Setup
\[ \text {Choose a generator } g \in_R G, \quad \text {Let } a \in_R \mathbb Z^*_p \text { be }SK \]
Commitment에 사용되는 Secret Key(SK)와 Public Key(PK)를 만듭니다. KZG Commitment은 타원 곡선의 Pairing 특성을 사용하기 때문에 \[ G\]에서 generator를 고르고, 랜덤한 값으로 비밀 키인 a를 고릅니다. 타원곡선 pairing 특성을 통해 G를 확장하면 \[ G_2\] 가 등장합니다.
\[ PK = \langle G,aG, a^2G…, a^tG, a^0G_2, a^1G_2\rangle \]
PK는 generator에 SK를 곱하면서 만듭니다. 이후 개인키는 사용하지 않기 때문에 폐기합니다.
이렇게 만든 PK를 혼자서 만드면 Prover가 가짜 증명을 만들 수 있기 때문에 여러 사람이 참여하여 PK를 만듭니다.
\[ \text {Choose random } a_1 \in_R Z^*_p \]
\[ PK = \langle a^0a_1^0G,a^1a_1^1G, a^2a_1^2G…, a^ta_1^tG, a^0a_1^0G_2, a^1a_1^1G_2\rangle \]
복잡한 SK를 Power of tau로 표현 할 수 있습니다.
\[ \tau^i = a_k^{i} * a_{k-1}^{i}, …a_{1}^{i}*a_{0}^{i} \]
\[ SK = \langle\tau^0,\; \tau^1,\; \tau^2, … \;\tau^t \rangle\]
\[ PK = \langle\tau^0G,\; \tau^1G,\; \tau^2G, … \;\tau^tG,\;\tau^0G_2,\; \tau^1G_2 \rangle\]
결론적으로 a를 아는 사람들이 담합을 하여 가짜 증명을 만드려 해도 한명의 a를 모르면 실패하게 되어 안전한 Scheme이 됩니다.
2. Commit
증명해야 하는 다항식을 \[ P(x) \]라고 할 때 Commitment 과정을 진행합니다.
알고 있는 다항식에 공개 검증키의 값을 넣으면 됩니다. 이 과정을 통해 다항식을 숨기지만 바꿀 수 없게 됩니다.
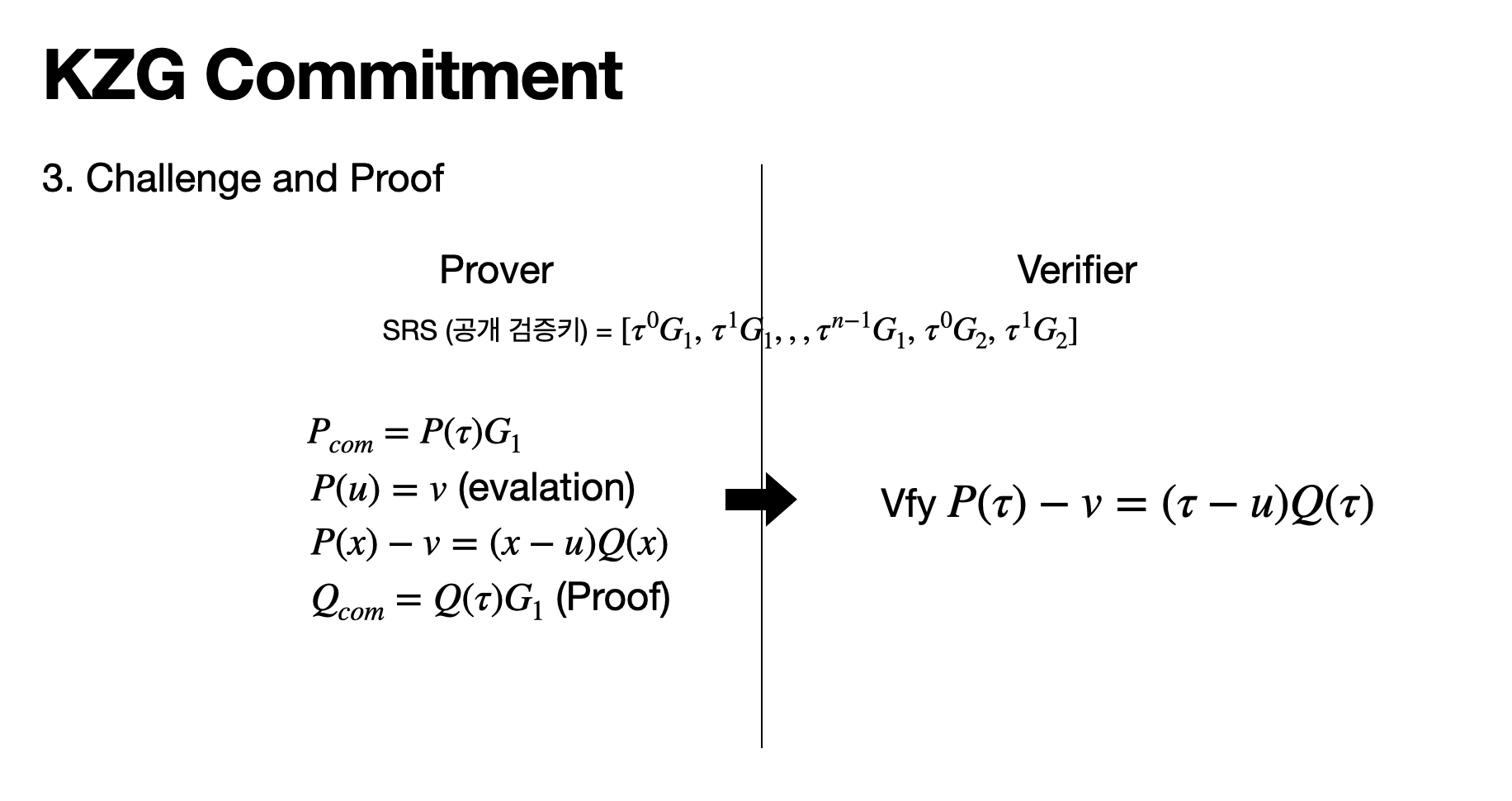
3. Challenge and Proof
Commit이 된 상태에서 Verifier는 Prover가 정확히 다항식을 아는지 test하기 위해 random 값 \[ u \]를 뽑아 Prover에게 Challenge 합니다.
Prover가 \[ P(u) = v \] 결과값인 v를 Verifier에게 전달합니다.
물론 이 과정은 Interactive 하기 때문에 Non-Interactive 하기 위해서 Fiat-Shamir transform를 사용하여 Challenge 값을 만듭니다.
\[u = H(pp | r ) \; (r \in_R \mathbb F)\]
Prover가 Challenge에 대해 evaluate 한 값이 실제로 맞는지 Verifier는 확인해야합니다.
그래서 Prover는 \[ P(x) - v = (x-u)Q(x) \]를 성립하는 Q(x)를 Commit하여 Proof로 Verifier에게 전달합니다.
\[Q_{com} = Q(\tau)G_1 \text { (Proof) }\]
Verifier는 Prover에게 받은 \[ P_{com}, Q_{com}, v \] 값을 통해 검증을 합니다.
4. Verify
Verifier는 \[ P(u) = v \] 가 성립하는지를 확인함으로 Prover가 \[P(x) \]를 알고 있는지 검증을 합니다.
검증 과정은 \[ P(u) = v \] 가 성립한다는 것은 \[P(x) - v = (x-u)Q(x)\]의 식이 성립하고, Commit에 사용된 값 \[\tau\] 를 넣어주면 \[P(\tau) - v = (\tau - u )Q(\tau)\] 다음과 같은 식이 됩니다.
이것을 검증하기 위해 타원곡선의 Pairing 성질을 활용해 \[e(G_1, G_2)^{P(\tau)-v} = e(G_1, G_2)^{Q(\tau)(\tau - u)}\] 가 성립하는지 확인합니다.
타원곡선의 Pairing은 다음과 같은 성질을 가집니다. \[e(aP, bQ) = e(P, bQ)^a = e(P, aQ)^b = e(P, Q)^{ab}\]
따라서 \[e((P(\tau) - v)G_1, G_2) = e(Q(\tau)G_1, \;(\tau-u)G_2)\] 이런 식이 되고 Prover가 전달해서 계산 가능한 \[P(\tau)G_1, vG_1, Q(\tau)G_1\] 과 공개 검증키를 통해 계산이 가능해집니다.
Further Study
- Poseidon Hash - paper
Non-interactive 하게 commit 하기 위해서 \[u = H(pp | r) \]로 생성, 기존 해시 함수는 ZK-friendly 하지 않아 Poseidon Hash 사용 - Pairings for beginners - link
타원 곡선의 pairing 특징… 짱짱 어려움 - PLONK - paper
R1CS의 방식과 달리 Permutation으로 변형하여 Constraints을 만듬. KZG의 trusted Setup 과정이 불필요
Reference
- Decipher ZK Class: youtube link
- Quadratic Arithmetic Programs: from Zero to Hero