An Introduction to STARK
Scalable and Transparent Zero-Knowledge Proofs
STARK
이번 글에서는 STARK에 대해 본격적으로 들어가기전에 STARK의 직관적 이해와 실제 적용 사례, 기존 증명의 차이점을 중점적으로 다룹니다.
STARK(Scalable, Transparent ARgument of Knowledge)는 SNARK에서 transparent 한 setup을 사용하는 기술입니다.
마찬가지로 컴퓨터 계산을 간단한 증명으로 바꾸어 검증을 하는데에 목표를 하고 있습니다.
Mechanics of a STARK
zk-SNARK와 비슷하게 복잡한 계산 과정을 산술화 (Arithmetization) 하고 다항식으로 만들어 컴파일 및 커밋 과정을 진행합니다.
하지만 이 과정에서 사용하는 기술들이 다르기 때문에 STARK는 신뢰할 수 있는 설정이 필요없고, 양자 컴퓨팅 공격에 저항력이 있습니다.
1단계: Arithmetization
피보나치 수열을 계산하는 프로그램의 계산 결과를 증명한다고 가정해봅시다.
\[F(i), F(i + 1)\] 이 input으로 주어졌을 때 \[F(i + 4)\] 의 값 증명하기 위해서는 계산 과정에서 피보나치 수열의 조건을 만족했고 중간 결과값이 뭐가 나왔는지를 증명해야합니다.
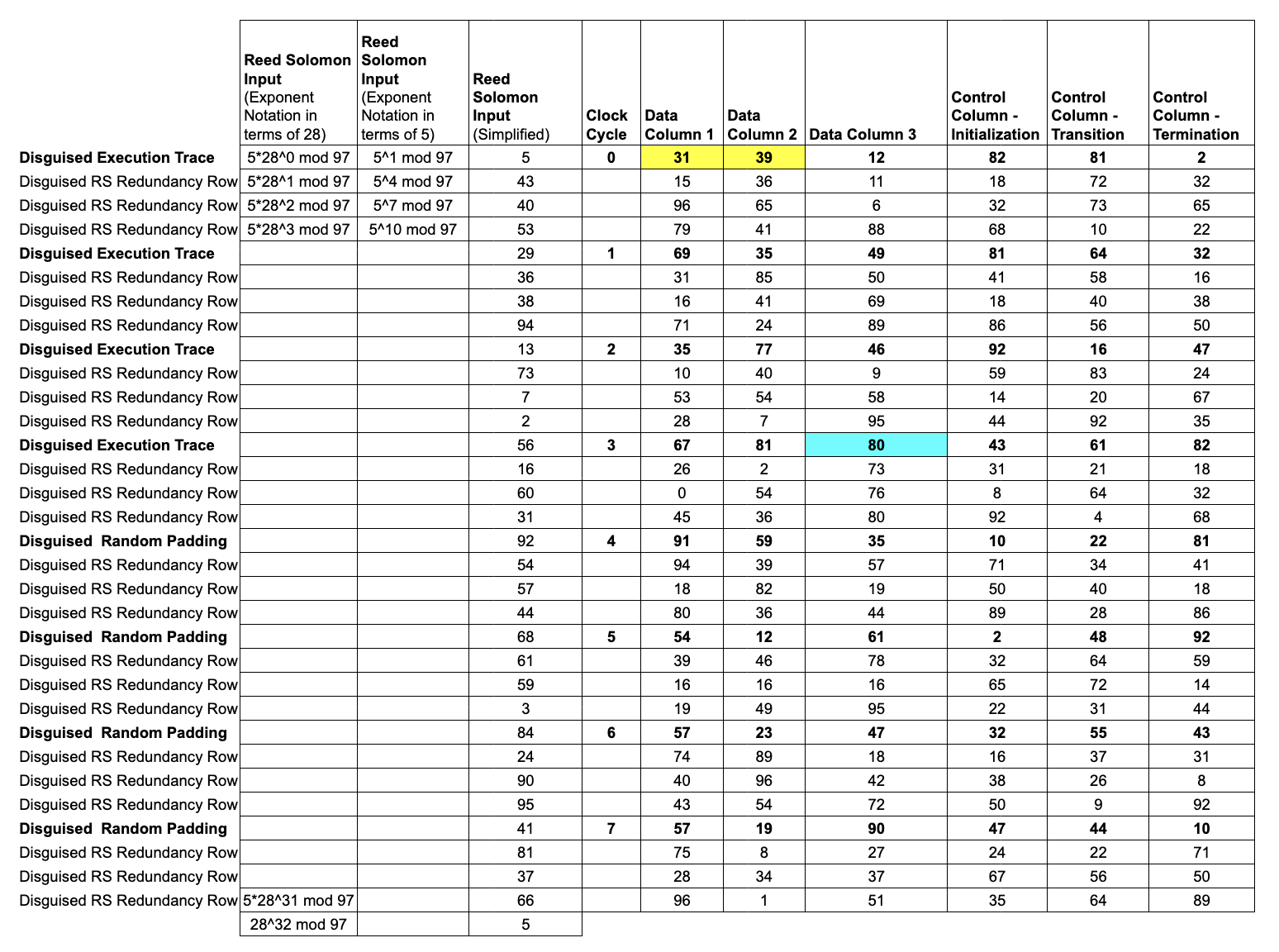
Execution trace라는 걸 통해 중간 결과가 무엇이 나왔는지 추적을 하고, 이 계산에는 제약 조건(constraints)가 뭐가 있고 만족했는지를 확인해야합니다.
여기서 중간 결과들을 Algebraic Execution Trace(AET)라고 부르며 제약 조건들의 집합을 Algebraic Intermediate Representation (AIR)이라 합니다
그래서 이 프로그램은 n번째 행의 상태가 (a_n, b_n)이라면, n+1번째 행의 상태는 반드시 (b_n, a_n + b_n)이어야 하는 전이 조건과, 계산의 처음과 끝이 입출력 값과 같은지 경계 제약을 검사해야 합니다.
INTT(Inverse Number Theoretic Transform) 를 이용해서 해당 column이 evaluation이 되는 다항식을 만듭니다. 여기서 평가 지점 x 는 원시 n차 단위근(root of unity) 로 \[\omega^n = 1\]을 만족하는 n개의 점입니다. Clock Cycle이 8개 있기 때문에 7차 이하의 다항식이 만들어집니다.
그럼 실행 중간 결과를 추적할 수 있는 trace polynomial이 만들어집니다.
여기서 이 평가 값 외에 다른 점을 추가로 해서 Reed-solomon encoding을 진행합니다. 기존의 점들이 \[5^{12*i} mod 97\]로 이루워진 8개의 점이었다면 \[5^{3*i} mod 97\] 인 32개의 점으로 확대하는 저차 다항식 확장(Low-Degree Extension)을 실행합니다.
여기서 해당 점들을 추가하여 prover의 계산 오류가 생기면 오류 증폭이 돼 검증이 효율적이게 됩니다.
이 단계의 결과물은 trace data를 trace polynomial로 만듭니다.
2단계: Commitment
1단계에서 얻은 trace polynomial을 통해 다항식이 바뀌지 않음을 증명하는 Commit을 진행해야 합니다.
Reed-solomon을 통해 증폭된 다항식에서 영지식 증명 속성 (중간 데이터 노출)을 만족하기 위해 shift를 통해 x 값 이동을 합니다.
trace-domain과 commitment-domain을 다르게 만드는 것인데, 만약에 같다면 random query 값에서 trace data가 나올 수 있습니다.
그리고 이 다항식을 Commit 하기 위해 각 값들을 해시하여 머클 트리의 leaf node로 만듭니다.
그래서 다항식의 머클루트를 만들어 commitment를 만들게 됩니다.
\[d_1\]의 경우 column에 있는 값들을 각각 해시하여 leaf로 만들어 \[d_1\]의 머클루트를 구합니다.
제약 조건이 \[t(g²x) - t(gx) - t(x) = 0\] 와 같을 경우 trace data가 들어가면 0이 나오는 제약 다항식을 만들 수 있습니다.
이때 여러개의 제약 다항식을 ALI(Algebraic linking IOP)를 이용하여 하나의 Mixing Constraint Polynomials을 만듭니다.
\[C(x) = \alpha_1^0 * c_0(x) + \alpha_1^1 * c_1(x) + \ldots \]
여기서 \[alpha\] 는 random하기 때문에 \[C(x)\] 가 유효하다면 개별 다항식도 유효하다고 할 수 있습니다.
제약 조건을 만족하는 trace를 넣었을 때 제약 다항식의 값이 0이 되어야 하기 때문에 Vanishing Polynomial(\[Z(x)\])을 만들어 몫 다항식(\[Q(x)\])를 만듭니다.
\[C(x) = Z(x) \cdot Q(x)\]
이 과정을 통해 증명자는 여러개의 제약 다항식을 trace data가 만족한다는 걸 증명하는 거 대신, 하나의 혼합 제약 다항식이 몫 다항식으로 분리되고 저차 다항식에 해당한다는 것을 증명하는 거로 바뀌게 됩니다.
3단계: FRI
앞과정에서 얻은 \[Q(x)\]를 Reed-solomon encoding으로 저차식 확장하여 나온 코드워드의 머클트리를 만듭니다.
이 \[Q(x)\]를 “Split-and-Fold”라는 기법으로 차수를 재귀적으로 줄여가며 결국 상수항의 커밋을 통해 증명을 진행합니다.
Prover가 commit한 다항식이 \[f_0(x) = 19 + 56x + 34x^2 + 48x^3 + 42x^4 + 37x^5 + 10x^6 +0x^7\] 일 경우
\[f_1(x) = f_{0, even}(x^2) + \gamma f_{0, odd}(x^2) \] 으로 나눕니다. 이때 \[\gamma\]는 prover가 무작위로 보냅니다.
\[f_1(x)\]에 대해 다시 LDE, commit을 하여 머클루트 값을 보내 commit을 합니다.
이 fold한 다항식하고, 머클루트 값이 일치하는지 확인하기 위해 verifier가 g 라는 랜덤 지점을 보냅니다.
\[f_{i- 1}(g), f_{i - 1}(-g)\] 값을 verifier에게 전달하면 이 지점이 머클루트를 통해 있는 점인지, 그리고 만든 \[f_{i}(x)\] 의 다항식이 일치하는지 확인합니다.
\[f_i(x^2) = f_{i - 1, even}(x^2) + \gamma_i f_{i - 1, odd}(x^2)\] 을 만족하기 때문에 이를 통해 다항식을 확인합니다.
이 과정을 반복하면 결국 상수항까지 접게 되어 검증을 하게 됩니다.
이 모든 과정을 거쳐 최종적으로 검증자가 단독으로 검증할 수 증명이 만들어집니다.
기존 기법과의 차이점
양자 암호가 등장한다면 SNARK는 결국 이산로그의 문제에 기반하여 보안을 보장하기 때문에 쉽게 풀릴 수 있습니다.
하지만 STARK는 commit 하는 과정에서 머클 트리에서 sha256 함수를 사용하기 때문에 해시 함수의 충돌 저항성으로 양자 암호로 쉽게 풀수 없습니다.
양자 컴퓨터가 ‘쇼어 알고리즘(Shor’s algorithm)’을 통해 타원 곡선 암호의 기반이 되는 이산 로그 문제를 완전히 풀어버리는 것과는 차원이 다른 문제입니다.
SNARK에서는 초기 setup에서 toxic waste를 통해 PK를 만들기 때문에 이 값이 노출된다면 보안에 영향을 줍니다.
하지만 STARK에서는 사전에 만든 공개키에 기반하여 commit 하지 않기 때문에 외부 신뢰 단계가 필요 없습니다.
실제 적용 사례
STARK는 Stark ware에서 만든 기술로 ZK-rollup 체인인 STARKNET, 디엡에서 사용하는 대규모 트렌젝션을 처리하는 STARKEX 등 적용되어 있습니다.
또한 zkvm인 Risk0에서 CPU 명령어 계산에 적용합니다.