Groth16: Verification Steps
Number of Operations, Reason for using Pairings
Groth16: Verification Steps
이 아티클에서는 Groth16의 Verification 과정과 사용되는 연산 수에 대한 설명, Pairing 연산을 사용하는 이유에 대해 설명하겠습니다.
Verification Step
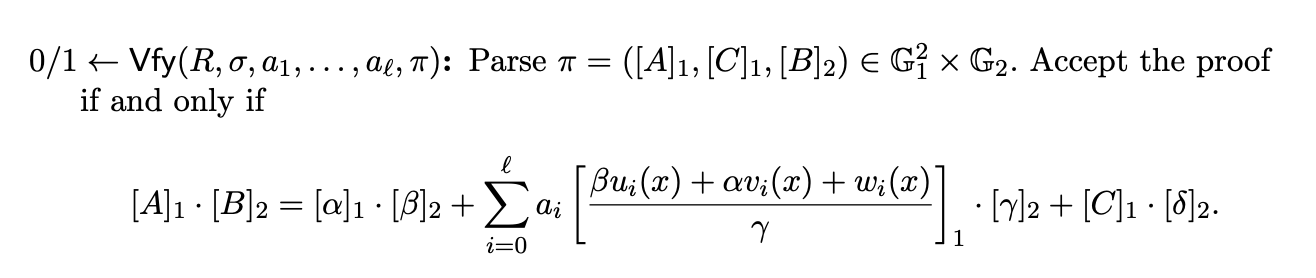
groth16 논문에 나와 있는 검증 과정입니다. 조금 더 자세하게 과정을 살펴보겠습니다.
1. Check the proof consists of three appropriate group elements.

먼저 받은 Proof가 각각의 그룹 원소에 속하는지 확인합니다.
만약 속하지 않는다면 증명이 거짓으로 처리됩니다.
\[[A]_1, [C]_1 \in \mathbb G_1, \; [B]_2 \in \mathbb G_2 \]
2. Computes \[ \ell \] exponetialtions in \[ \mathbb G_1 \]
CRS에서 받은 \[ \left[\frac{\beta u_i(x) + \alpha v_i(x) + \omega _i(x)}{\gamma }\right] _1 \] 를 이용하여 \[ \sum_{i = 0}^{\ell}a_i\left[\frac{\beta u_i(x) + \alpha v_i(x) + \omega _i(x)}{\gamma }\right] _1 \] 식을 계산합니다.
이때 \[ [a_1, a_2, … a_{\ell}] \] 는 “public portions of the witness” 으로 witness 중 일부를 public input으로 공개합니다.
이를 통해 witness 중 [1, 2, x, … ,x_n] input이 1, 2일 때 해당하는 x를 알고 있다라고 할 수 있습니다.
이 과정에서 \[\ell\]번의 스칼라 곱셈이 진행됩니다.
3. Check the Pairing Equation
위와 같은 식이 성립하는지 검증을 진행합니다. \[ [\alpha]_1 \cdot [\beta]_2 \]는 CRS에 포함되기 때문에 총 3번의 pairing 연산이 진행됩니다.
이 식이 성립하면 증명이 참이 됩니다.
뒤에서 이 페어링 연산이 무엇인지 왜 사용하는지 더 살펴보도록 하겠습니다.
Verify: Number of Operations
groth16은 위의 표와 같이 Proof의 크기를 3개의 그룹 원소로 줄이고, 증명 과정의 연산의 수도 줄여 가볍고 빠른 증명이 가능합니다.
그럼 어떻게 groth16이 이전과 다르게 바뀌게 되었는지 알아보겠습니다.
Before Groth16 (Pinocchio Protocol)
기존의 방법인 PHGR13(Pinocchio)에서는 Proof가 거짓 증명자가 만들어낸것이 아닌지 확인하기 위해 Knowledge of Exponent Assumption (KOE) 방법을 사용합니다.
KOE는 \[\alpha \]-pair 인 (a, b)가 주어졌을 때 (\[b = a^\alpha \]) 또다른 pair인 (a’, b’)를 만들면, ( \[a’ = a ^ r, b’ = b ^ r, b’ = (a ^{\alpha})^{r} \] )로 계산했음을 확실할 수 있습니다.
즉 CRS로 받은 \[E(a_i(s)), E(\alpha_Aa_i(s))\]를 통해 Proof \[E(\sum_{i=1}^{n}s_ia_i(s)),\; E(\sum_{i=1}^{n}s_i \alpha _A a_i(s)) \] 를 만들었다면 prover는 \[s_i\]를 알고 있음을 확인 할 수 있습니다.
따라서 이 Scheme에서의 Proof는 각 값을 올바르게 만들었다는 근거까지 포함하여 많은 증명수를 갖게 됩니다.
증명을 검증하는 단계에서도 증명이 조작되지 않았음을 검증, 증명을 합쳐서 원래 계산식이 일치하는지 검증을 진행하여 더 많은 연산을 진행하게 됩니다.
Proof 검증하는데 8개의 pairing 연산, 검증 식 계산에 3개의 pairing 연산이 사용되고, Pairing Product Equation(PPE) 연산도 5번을 진행합니다.
Groth16
Groth16도 제출된 증명(Proof)이 위조된 것은 아닌지 검증하는 과정을 포함해야 합니다.
위 사진과 같은 식이라면 \[ [A]_1, [C]_1 = G_1, [B]_2 = G_2\] 이라 조작을 하면 해당 식은 성립됩니다.
거짓 prover가 Proof을 조작하지 못하도록 랜덤값인 \[\alpha, \beta \] 을 추가하고 CRS에서 \[[\alpha]_1, [\beta]_2\] 를 계산합니다.
\[\alpha, \beta \]를 모르기 때문에 임의값을 조작하여 식을 성립하게 만들 수 없습니다.
Proof에 랜덤값이 추가되어 계산을 하도록 만들고, \[ r, s\]는 salt 값으로 같은 witness일 때 다른 증명 값이 나오도록 만들어 증명으로 부터 witness을 추측할 수 없도록 만듭니다. (zero-knowledge)
따라서 groth16은 기존과 다른 방식으로 Soundness를 보장하여 3그룹 원소의 증명, 3개의 pairing 연산과 1번의 PPE 계산으로 간결하게 검증 가능합니다.
Pairing function
Proof로 받는 \[ [A]_1, [B]_2, [C]_1\]의 값은 타원곡선 상의 점으로 이 값을 통해 A, B, C의 값을 알 수 없습니다.
또한 타원곡선은 덧셈 연산에서만 동형사상을 갖기 때문에 commit된 값의 곱셈을 구할 수 없습니다.
이런 한계를 극복하기 위해 쌍선형(Bilinearity) 성질을 가진 pairing 함수를 이용하여 계산을 할 수 있습니다.
Pairing Property
Tate Pairing 함수는 페어링이라는 수학적 개념을 실제로 구현한 알고리즘의 한 종류입니다.
두 개의 타원곡선 위의 점 \[P, Q\]를 입력 받아 \[\mathbb G_T\]의 원소를 출력하는 함수입니다.
Pairing의 성질인 쌍선형 성질은 두개의 입력값(x, y)가 각각 선형성을 가진다는 뜻입니다.
페어링의 한쪽 입력값에 덧셈이 있을 경우 이를 각각 페어링한 결과의 곱셈으로 분리할 수 있습니다.
\[e(P_1 + P_2, Q) = e(P_1,Q) \cdot e(P_2, Q) \]
이런 덧셈 성질로부터, 입력값에 곱해진 스칼라 값들은 페어링 결과의 지수로 옮겨져 곱해집니다.
\[e(aP, Q) = e(P_1 + P_2 +… + P_a ,Q) = e(P,Q)^a\]
Pairing 함수의 성질를 만족하는 쌍선형 함수 예시로 \[e(x,y) = 2^{xy} \]가 존재합니다.
해당식은 위와 같이 성질을 만족하는 것을 볼 수 있습니다.
모든 타원곡선 함수들이 pairing에 특화되어 있지는 않습니다. 타원곡선의 embedding degree 라는 것이 있는데 이거에 따라 pairing-friendly elliptic curve라고 불리웁니다.
자주 사용하는 함수는 BLS12-381 함수로 12가 embedding degree고 381이 prime field size입니다.
groth16에서는 효율성을 위해 그룹이 서로 다른 비대칭 쌍선형 그룹의 pairing 연산을 사용합니다.
\[G_1\]에서 field를 확장하여 \[G_2\]를 구합니다. \[F_p^k\]에서 만족하는 \[G_2\]가 구해집니다. (k = embedding degree)
페어링 연산의 결과는 \[G_T\]에 해당하며 \[G_T\]는 스칼라 그룹에 해당합니다.
따라서 페어링 연산의 결과값은 스칼라 값이 나오게 됩니다.
Pairing code (SageMath)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
from sage.all import *
p = Integer(7549); A = Integer(0); B = Integer(1); n = Integer(157); k = Integer(6); t = Integer(14)
F = GF(p)
# y^2 = x^3 + 1
E = EllipticCurve(F, [A, B])
# make ring
R = F['x'];
(x,) = R._first_ngens(1);
K = GF((p,k), modulus=x**k+Integer(2), names=('a',));
(a,) = K._first_ngens(1)
# extend curve using K
# F(p^k)
EK = E.base_extend(K)
# define points
P = EK(Integer(3050), Integer(5371)); # G1
Q = EK(Integer(6908)*a**Integer(4), Integer(3231)*a**Integer(3)) # G2
# compute pairing
# print(P.ate_pairing(Q, n, k, t))
# test pairing properties
s = Integer(randrange(Integer(1), n))
print('P = ', P)
print('Q = ', Q)
print('s = ', s)
print('\n--- 페어링 속성 테스트 ---')
# 1. e(P, Q) 계산
e_P_Q = P.ate_pairing(Q, n, k, t)
print('e(P, Q) =', e_P_Q)
# 2. e(P, Q)^s 계산 (쌍선형성의 한쪽)
e_P_Q_s = e_P_Q**s
print('e(P, Q)^s =', e_P_Q_s)
# 3. e(s*P, Q) 와 e(P, s*Q) 계산 (쌍선형성의 다른쪽)
# 이 값들이 바로 위에서 계산한 e(P, Q)^s 와 같아야 합니다.
e_sP_Q = (s*P).ate_pairing(Q, n, k, t)
e_P_sQ = P.ate_pairing(s*Q, n, k, t)
print('e(s*P, Q) =', e_sP_Q)
print('e(P, s*Q) =', e_P_sQ)
# 4. 모든 값이 같은지 최종 확인
print('\n--- 결과 검증 ---')
print('e(s*P, Q) == e(P, Q)^s :', e_sP_Q == e_P_Q_s)
print('e(P, s*Q) == e(P, Q)^s :', e_P_sQ == e_P_Q_s)
페어링 연산을 SageMath를 이용하여 계산을 해보았습니다.
타원곡선 E를 만든 후 확잔된 타원곡선인 EK를 만듭니다.
EK와 E에 모두 속하는 P와 EK의 점인 Q를 설정하여 해당 pairing 연산이 같은 값이 나오는지 확인합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
sage -python pairing.py
P = (3050 : 5371 : 1)
Q = (6908*a^4 : 3231*a^3 : 1)
s = 75
--- 페어링 속성 테스트 ---
e(P, Q) = 6708*a^5 + 4230*a^4 + 4350*a^3 + 2064*a^2 + 4022*a + 6733
e(P, Q)^s = 2484*a^5 + 143*a^4 + 7249*a^3 + 4560*a^2 + 436*a + 4966
e(s*P, Q) = 2484*a^5 + 143*a^4 + 7249*a^3 + 4560*a^2 + 436*a + 4966
e(P, s*Q) = 2484*a^5 + 143*a^4 + 7249*a^3 + 4560*a^2 + 436*a + 4966
--- 결과 검증 ---
e(s*P, Q) == e(P, Q)^s : True
e(P, s*Q) == e(P, Q)^s : True
따라서 \[e(sP,Q) = e(P, sQ) = e(P,Q)^s\]가 성립함을 볼 수 있습니다.
최소 증명 사이즈
효율적인 SNARK를 위해 최소 증명 사이즈로 맞춰야 합니다.
먼저 선형으로 이루어진 증명식이라면 악의적인 증명자가 쉽게 증명을 조작할 수 있어 qudratic으로 만들어야 합니다.
비대칭 쌍선형 그룹에서 이차식으로 증명식을 만들었다면 페어링 연산을 할 때 두 소스 그룹의 원소 (G1, G2) 가 모두 있어야 합니다.
따라서 각각 그룹의 원소가 1개씩 있는 경우가 존재하는지 아직 모르지만 현재까지는 groth16의 3개의 그룹원소 증명이 최적화되어 있습니다.
Further Study
- Pairings for beginners - link
타원 곡선의 pairing 특징… 짱짱 어려움